heap

Data Structures and Algorithms

6.2 Heaps

Heaps are based on the notion of a complete tree, for which we gave an informal definition earlier.
Formally:
A binary tree is completely full if it is of height, h, and has 2^h+1-1 nodes.
A binary tree of height, h, is complete iff

1. it is empty or
2. its left subtree is complete of height h-1 and its right subtree is completely full of height h-2 or
3. its left subtree is completely full of height h-1 and its right subtree is complete of height h-1.

A complete tree is filled from the left:

• all the leaves are on
  • the same level or
  • two adjacent ones and
• all nodes at the lowest level are as far to the left as possible.

Heaps

A binary tree has the heap property iff

1. it is empty or
2. the key in the root is larger than that in either child and both subtrees have the heap property.

A heap can be used as a priority queue: the highest priority item is at the root and is trivially extracted. But if the root is deleted, we are left with two sub-trees and we must efficiently re-create a single tree with the heap property.

The value of the heap structure is that we can both extract the highest priority item and insert a new one in O(logn) time.

How do we do this?

Let's start with this heap.A deletion will remove the T at the root.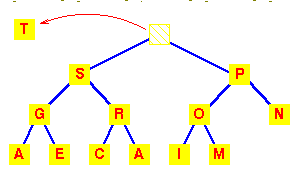

To work out how we're going to maintain the heap property, use the fact that a complete tree is filled from the left. So that the position which must become empty is the one occupied by the M.Put it in the vacant root position.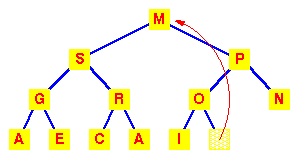

This has violated the condition that the root must be greater than each of its children.So interchange the M with the larger of its children.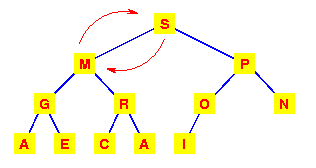

The left subtree has now lost the heap property.So again interchange the M with the larger of its children.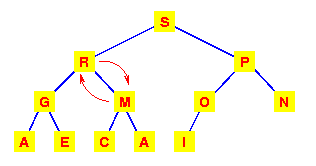

This tree is now a heap again, so we're finished.
We need to make at most h interchanges of a root of a subtree with one of its children to fully restore the heap property. Thus deletion from a heap is O(h) or O(logn).

Addition to a heap

To add an item to a heap, we follow the reverse procedure.Place it in the next leaf position and move it up. Again, we require O(h) or O(logn) exchanges.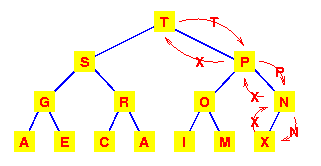

---

Storage of complete trees

The properties of a complete tree lead to a very efficient storage mechanism using n sequential locations in an array.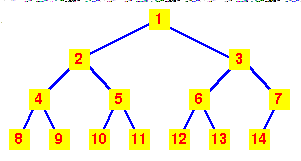

If we number the nodes from 1 at the root and place: the left child of node k at position 2k the right child of node k at position 2k+1 Then the 'fill from the left' nature of the complete tree ensures that the heap can be stored in consecutive locations in an array.

Viewed as an array, we can see that the nth node is always in index position n.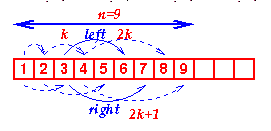

The code for extracting the highest priority item from a heap is, naturally, recursive. Once we've extracted the root (highest priority) item and swapped the last item into its place, we simply call MoveDownrecursively until we get to the bottom of the tree.